巧用“思考题”培养学生数学核心素养
驻马店实验小学 郝秀丽
在学生学完分数的基本性质和通分之后,人教版实验教材安排了一道思考题,在备课时预设了学生可能想到的三种方法,而在实际教学中却“节外生枝”,我巧妙的利用这一生成资源,培养学生的数学核心素养。习题如下:
看到题目后,大多数学生纷纷在练习本上写着、算着,不一会儿,一些学生脸上轻松的表情和坐正的姿势告诉我交流可以拉开序幕。
生1:我用的通分的方法,因为分母是互质数,所以通分后是5/20和4/20,没有找到符合的分数,继续通分得到10/40、8/40找到这个分数是9/40 。(在备课中我预设到这种方法也是大多数孩子都能想到。)
生2:我把这两个分数化成小数,0.25和0.2, 0.24在两个小数之间,再把0.24化成百分数是24%,再化简为6/25 。
师:除了0.24,你还能想到哪些适合的小数。先独立思考,和同桌交流想法。(我适时的提出了一个问题)
用这种方法思考的孩子发表了自己的观点。
师:谁还有不同的想法?
生3:还可以利用分数的基本性质把分子分母同时乘以2,得到分数 2/9。(这正是我最希望出现的一种思路,我把他的发言写到黑板上,目的是让学生都能用这种最简的思路来解决)
教学都在我的预设中,正打算结束这道思考题的交流,进行下个环节的学习,此时,我们班的田源高举着手,多年的教学经验告诉我,这样的孩子一定有话要说。我示意他说,这孩子三步并作两步上了讲台,他指着刚才第三个孩子的发言(我的板书)
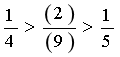
,说:我有个猜想, 用分子加分子,用分母加分母,边说边在我的板书上连着。他的发言出乎我的意料,我大脑飞速的旋转,我预感到田源的猜想是极具价值的,于是借题发挥,
说到:同学们,先用田源的发现,先来猜一猜,
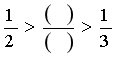
然后实际算一算,看看这个猜想是否正确?
经过验证孩子们发现田源的猜想成立,此时我又抛出了一个问题:
请你自己举一个例子,和同桌交流这样填的理由,把你发现的规律在四人小组内交流,并用自己喜欢的语言描述出来。(小组讨论后,全班交流)
生4: 分子是1,分母是相邻的两个自然数,可以用分子加分子得分子,分母加分母得分母的方法找到这两个分数之间的分数。
师:表述的很准确,谁能用更简洁的语言来表述这一发现。
生6:分子是1,分母互质的两个分数,用分子加分子,分母加分母的方法可得出它们之间的分数。
生7:其实这两个分数就是相邻的两个分数单位。我们“用分子加分子,分母加分母的方法就可以找到两个相邻的分数单位之间的分数。”(教室里响起学生们自发的掌声,我读懂他们的掌声是对生7数学语言的准确和简洁的欣赏。)
师:我们能否用一种更简洁、更明了的表示方法来总结这一规律,
(这个问题的诞生是受到第7个孩子发言的启示)先独立思考,然后前后四人交流。(我走到学生参与他们的交流)
生7:
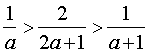
生8:利用分数的基本性质,我们可以找到许许多多这样的分数,
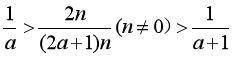
(教室里再一次响起孩子们热烈的掌声)
我按耐不住自己的激动和兴奋,激情四溢的总结道:同学们,通过大胆猜想、小心验证,我们归纳出“找两个相邻的分数单位之间分数的方法”,这节课我和大家一起经历了一段奇妙的数学之旅,发现了一个数学奥秘,大家想一想,是谁给我们打开了这扇神奇的大门,“田源”同学们异口同声的喊道,“今天的这个数学规律我们就用“田源”的名字命名”。我激动的向全体同学宣布,并把“田源规律”四个字郑重的写到板报的“每日一星”中,教室里响起孩子们雷鸣般的掌声。
【思考】
南京大学郑毓信教授说:“数学学习的一个主要价值就是有利于人们思维方式的改进,并能使人们逐步学会更清晰、更合理、更深入地思考问题。”可见,思维是数学能力的核心,思维也是数学素养的灵魂。在上述案例中,首先是由田园同学发现和提出问题。他的大胆猜想为后面的交流碰撞,思考探究提供了素材,也为全体学生一起经历这段奇妙的思维旅程开启了“闸门”。猜想是一种创造性思维方式,在教学实践中,教师要鼓励学生勇于质疑、不盲从,勇于发表自己的观点,为学生大胆猜想提供沃土;笔者顺水推舟借用这一猜想,引导每一位学生都举一个例子来验证这一猜想,在根据每一位学生不同的思维特点和思维水平,引导学生尝试着用自己的语言来描述自己的发现,学生在独立思考后将自己与他人的总结进行比较,不断反思、不断完善,最后概括出“用分子加分子,分母加分母的方法就可以找到两个相邻的分数单位之间的分数。”这一思维活动过程培养和发展了学生的严谨意识和理性精神。教育哲学理论认为,“学习知识对于人类而言不仅意味着实际的用途,也意味着理智的欢乐——一种经过严肃认真地思考后豁然开朗的情感体验。这种理智的欢乐对于学习者的吸引力要超越任何外在的奖赏”;最后引导学生用最简洁、明了的字母式子来表达这一规律。由于学生在五年级上册已经学习了用字母表示数、数量关系以及简易方程,我灵活应对设计了用最简洁、最明了的方式来表示这一规律的问题,以引导学生的抽象思维水平带到更高的层次。这节课,以一道思考题为载体,以学生的猜想为契机,笔者引导全体学生从特殊到一般,从感性到理性,引导学生抽象出这一规律的字母式子,培养了学生数学素养。
(该篇文章发表在2017年3月《小学教学(数学版)》)


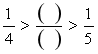
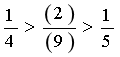 ,说:我有个猜想, 用分子加分子,用分母加分母,边说边在我的板书上连着。他的发言出乎我的意料,我大脑飞速的旋转,我预感到田源的猜想是极具价值的,于是借题发挥,
,说:我有个猜想, 用分子加分子,用分母加分母,边说边在我的板书上连着。他的发言出乎我的意料,我大脑飞速的旋转,我预感到田源的猜想是极具价值的,于是借题发挥,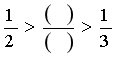 然后实际算一算,看看这个猜想是否正确?
然后实际算一算,看看这个猜想是否正确?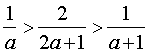
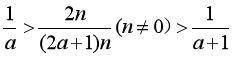 (教室里再一次响起孩子们热烈的掌声)
(教室里再一次响起孩子们热烈的掌声)