教材分析：

　　

　　本节课是苏教版六年级数学下册“图形与几何”中“平面图形的面积”整理与复习，在此之前，学生已经掌握了长方形、正方形、平行四边形、三角形、梯形、圆这几种基本图形的特征，并学会了其面积的计算方法，在推导面积公式的过程中也已感受到了转化思想的作用。本节课要启发学生回顾面积公式的推导过程，理清它们之间的联系，帮助学生建构知识网，发展学生的空间观念。

　　

　　教学目标：

　　

　　1.通过复习，进一步理解并掌握平面图形面积的计算方法，以及面积公式的推导过程。通过回顾梳理平面图形面积的计算公式，借助转化方法，沟通面积间内在的联系。

　　

　　2.通过引导学生探索知识间的相互联系，培养学生梳理知识综合、概括能力。

　　

　　3.渗透事物之间是相互联系的的辩证唯物主义观点和转化的数学思想。

　　

　　教学重难点：

　　

　　教学重点：复习平面图形面积计算公式及推导过程，并能熟练的应用公式进行计算。

　　

　　教学难点：理解平面图形面积计算公式的推导过程及内在联系。

　　

　　教具准备：

　　

　　多媒体课件，六个平面图形。

　　

　　教学过程：

　　

　　一、揭示课题

　　

　　谈话：回忆，在小学阶段学习过哦哪些平面图形，今天这节课，我们复习平面图形的有关知识。

　　

　　板书课题：平面图形面积复习

　　

　　二、自主整理

　　

　　1.根据复习提纲自主整理并和同桌交流

　　

　　（1）面积的含义什么？

　　

　　（2）这些平面图形的面积计算公式是什么？用字母该如何什么？

　　

　　（3）平面图形的面积计算公式是怎样推导的？

　　

　　2.学生汇报交流结果：长方形、正方形、平行四边形、三角形、梯形、圆的面积推导过程，渗透转化思想。

　　

　　学生汇报完后，课件逐一演示这些平面图形面积的推导过程。

　　

　　在演示三角形的面积计算公式的推导时介绍“半广以乘正从”的方法。

　　

　　三、构建知识网络图

　　

　　1.整理平面图形之间的联系。

　　

　　引导：为什么长方形的面积计算是其他平面图形面积计算公式推导的基础？

　　

　　讨论：这些平面图形之间有什么联系？请同学们在小组内讨论。

　　

　　学生按照要求活动，教师巡视。

　　

　　2.小组汇报交流、展示。

　　

　　3.明确平面图形之间的联系，建立知识网络图。

　　

　　小结：我们把零散的知识归纳整理成了一个完整的知识体系，其实平面图形的面积还可以用知识树的方法来进行整理。

　　

　　4.介绍知识树。

　　

　　四、练习与实践

　　

　　1. 求下列图形的面积

 

　　

　　2.判断

　　

　　（1）一个三角形，底6分米，高5分米，它的面积是30平方分米。（     ）

　　

　　（2）一个圆，直径是2厘米，它的面积是12.56厘米。（     ）

　　

　　（3）两个等底等高的三角形，它们的面积肯定相等。（     ）

　　

　　（4）两个面积相等的梯形可以拼成一个平行四边形。（     ）

　　

　　3. 智力大比拼

　　

　　（1）长方形的面积是多少？

　　

　　（2）在长方形里剪一个最的正方形，正方形的长是多少？面积是多少？

　　

　　（3）在长方形里剪一个最大的的三角形，三角形的底和高分别是多少？面积是多少？

　　

　　（4）在长方形里剪一个最大的圆，圆的直径是多少？面积是多少？

　　

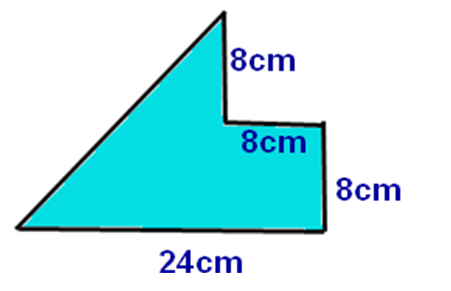
　　4、求组合图形的面积

 

　　

　　五、全课总结

　　

　　通过今天这节课的复习，你有什么新的收获？

　　

　　板书设计：

　　

　　平面图形的面积复习